Теория графов

Теория

Тео́рия гра́фов — раздел дискретной математики, изучающий графы, одна из ветвей топологии. Граф — это один из способов графического представления информации, отражающий количество объектов изучаемой системы и взаимосвязи между ними.

Объекты, отражённые в графе, представлены в нём как вершины (узлы) графа, а связи между ними — как дуги (рёбра). Таким образом, граф представляет собой совокупность непустого множества вершин и множества связей между вершинами.

Количество вершин графа называют его порядком. Количество рёбер называют размером графа.

Рёбрам графа могут быть сопоставлены числовые значения, которые называют размером графа.

Рёбрам графа могут быть сопоставлены числовые значения, которые называют весами рёбер. Например, вес ребра в графе, обозначающем дорожную сеть, может представлять собой длину соответствующей дороги между вершинами графа, обозначающими населённые пункты. Граф, рёбрами которого назначены значения весов, называют взвешенным.

Две вершины называют концевыми вершинами(концами) ребра, которое их соединяет. При этом говорят, что ребро инцидентно каждой из соединяемых им вершин и, наоборот, каждая концевая вершина называется инцидентной соединяющему их ребру. Две концевые вершины одного и того же ребра называют соседними.

Рёбра, имеющие общую концевую вершину, называют смежными.

Рёбра, инцидентные одной и той же паре вершин (т.е. соединяющие одну и ту же пару вершин), называют кратными, или параллельными. Граф с кратными рёбрами называют мультиграфом.

Ребро, концами которого являются одна и та же вершина, называется петлёй. Граф, содержащий петли (и кратные рёбра), называют псевдографом.

Степенью вершины называют количество инцидентных ей (исходящих из неё) рёбер, при этом петли, замкнутые на эту вершину, входят в подсчёт дважды.

Вершина называется изолированной, если она не является концом ни для одного ребра. Вершина называется висячей(листом), если она является концом ровно одного ребра.

Пустой граф — граф, состоящий из произвольного количества изолированных вершин (т.е. не имеющий рёбер).

Полный граф — граф, не имеющий петель и кратных рёбер, в котором каждая пара вершин соединена ребром.

Путь(цепь) в графе — конечная последовательность вершин, каждая из которых (кроме последней) соединена со следующей вершиной ребром. Циклом называют путь, в котором первая и последняя вершины совпадают. Путь (или цикл) называют простым, если рёбра в нём не повторяются. Простой путь(цикл) называют элементарным, если вершины в нём не повторяются.

Длиной пути (или цикла) называют количество составляющих его рёбер.

Связный граф — граф, в котором для любых двух вершин существует связывающий их путь.

Сильно связный граф — ориентированный граф, в котором существует маршрут из любой вершины в любую другую.

Неориентированный граф

В неориентированном графе связи между любыми парами концевых вершин являются двунаправленными, т.е. эти концевые вершины "равноправны" по отношению к этой связи.

Пример неориентированного графа:

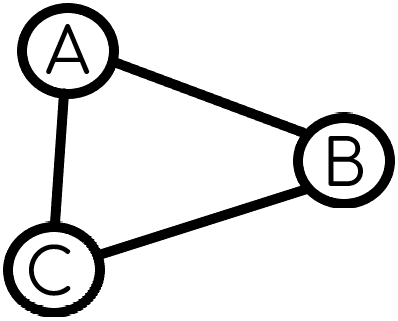
Ориентированный граф (орграф)

В ориентированном графе связи между концевыми вершинами являются направленными. Рёбра ориентированного графа называют дугами. Пути в ориентированном графе называют маршрутами(ориентированными путями). Замкнутый путь(цикл) в ориентированном графе называют контуром. Ориентированный граф, в котором каждая пара концевых вершин связана только одной дугой, называют направленным (в отличие от него в простом ориентированном графе какие-то вершины могут быть соединены двумя дугами, имеющими противоположные направления). Полный направленный граф называют турниром. Ориентированный граф, полученный из исходного путём смены направлений рёбер на противоположные, называют обратным.

Пример ориентированного графа (является направленным, турниром):

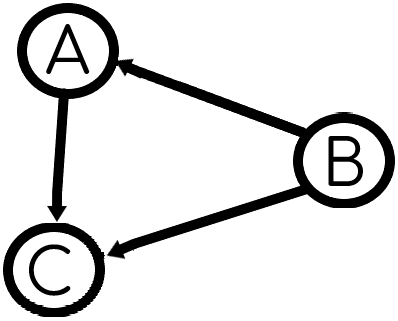
Дерево

Дерево — граф, в котором существует один-единственный путь между любой парой вершин и не имеется ни одного цикла. Ориентированное(направленное) дерево — орграф, в котором существует один-единственный маршрут между любой парой вершин и не имеется ни одного контура. Одна из вершин дерева (его корень) не имеет входящих в неё дуг, а все остальные вершины имеют ровно одну входящую дугу. При этом вершины, не имеющие исходящих из них дуг, называются листьями.

Пример дерева:

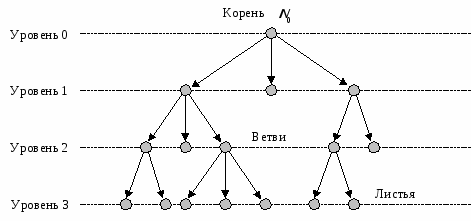
Двоичное дерево — ориентированное дерево, в котором для каждой вершины количество исходящих из неё дуг не превосходит двух.

Способы представления графов

1. Графический способ — изображение графа. Пример:

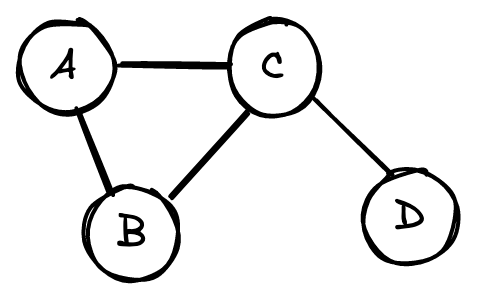
2. Список рёбер — перечисление всех рёбер графа как пар обозначений связываемых этими рёбрами вершин. Пример: {A,B}, {A,D}, {A,C}, {B,C}, {C,D}.
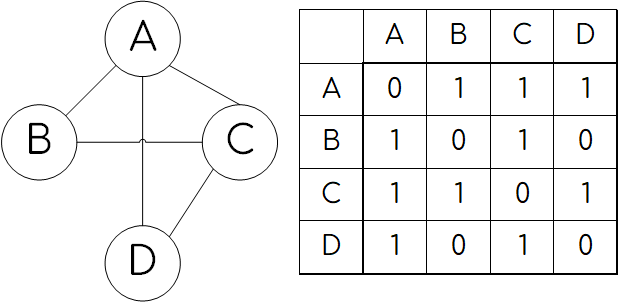
3. Матрица смежности — квадратная симметричная таблица(матрица), в которой столбцы, и строки соответствуют вершинам графа, а в ячейках на их пересечении записываются числа, обозначающие наличие или отсутствие связей между соответствующими парами вершин (обычно — количество связей между вершинами). В простейшем случае, когда граф не имеет кратных рёбер и петель, матрица смежности содержит единицы для ячеек, соответствующих парам вершин, связанных ребром, и нули — для несвязанных вершин. Пример:

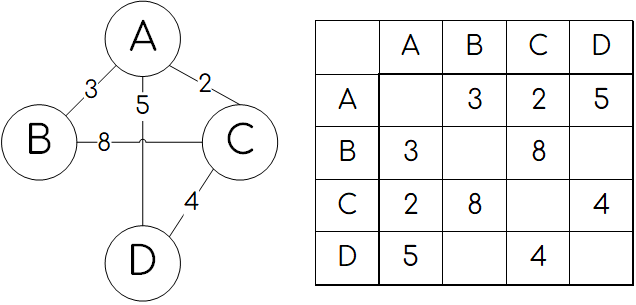
Для взвешенного графа возможен вариант матрицы смежности, где в ячейках записываются веса рёбер или нули (либо ячейки оставляются пустыми). Пример:

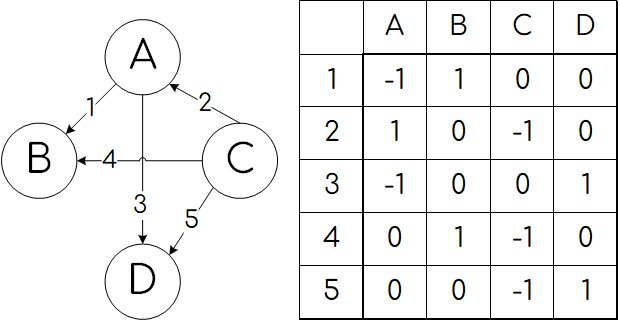
4. Матрица инцидентности — таблица, столбцы которой соответствуют вершинам, а строки — рёбрам. При этом в ячейках на их пересечении записываются числа:

• для неориентированного графа — число 1, если данная вершина инцидентна данному ребру, или 0 — в противном случае;
• для ориентированного графа — число -1, если данная дуга исходит из данной вершины, число 1, если данная дуга входит в данную вершину, число 2, если дуга представляет собой петлю, или 0 — в противном случае. Пример:

Заключение

Теория графов очень много где применяется: при решении задач, в написании программ, в представлении различных объектов и связей между ними. Графы и деревья – основные структуры данных. Спектр их применения огромен. Например, графы используются там, где необходим алгоритм поиска решений. Реальный пример их использования – sea-of-nodes JIT-компилятора, алгоритмы поиска пути на картах. Деревья используются тогда, когда мы должны произвести быстрое добавление/удаление объекта с поиском по ключу. Например, в различных словарях и индексах Баз данных. Кроме того, деревья являются неотъемлемой частью случайного леса – алгоритма машинного обучения. И конечно существует ещё множество примеров при решении задач в олимпиадном программировании, в различных алгоритмических конструкциях.