Теория
Кодирование символов обычно предполагает, что каждому символу всегда сопоставляется одинаковое количество битов (например, в кодовой таблице ASCII каждому символу сопоставляется один байт, хранящий порядковый номер того или иного символа в этой таблице). Такой способ кодирования прост и удобен, однако очевидно, что он является не самым оптимальным.
Для значительной части символов используются не все биты отведённых под них байтов (часть старших битов — нулевые), а при наличии в тексте только части символов, предусмотренных в таблице ASCII (например, если текст содержит только прописные русские буквы), приходится всё равно использовать 8-битный код.
Более компактным является неравномерный двоичный код (особенно если при его построении исходить из частоты встречаемости различных символов и присваивать наиболее часто используемым знакам самые короткие коды, как это сделано в методе Хаффмана). При этом количество битов, отводимых для кодирования символов, в целом зависит от количества используемых в конкретном случае различных символов (от мощности алфавита), а коды, соответствующие разным символам, могут иметь различную длину в битах.
Главное при таком кодировании — обеспечить возможность однозначного декодирования записанной с помощью этих кодов строки (поочерёдного, слева направо, выделения и распознавания из сплошной последовательности нулей и единиц кодов отдельных букв). Для этого коды символам необходимо назначать в соответствии с условиями Фано.
Прямое условие Фано
Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с началом (префиксом) какого-либо другого, более длинного кода.
Примеры:
| A | B | C |
|---|---|---|
| 10 | 11 | 001 |
D: 00 недопустимо из-за того что код D совпадает с началом кода C (C: 0 0 1, D: 0 0);
| A | B | C |
|---|---|---|
| 10 | 11 | 00 |
D: 11 недопустимо из-за того что код D совпадает с кодом B (B: 11, D: 11);
| A | B | C |
|---|---|---|
| 100 | 110 | 010 |
D: 00 допустимо. Код D не совпадает ни с одним другим кодом и с началом никакого другого кода.
Обратное условие Фано
Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с окончанием (постфиксом) какого-либо другого, более длинного кода.
Примеры:
| A | B | C |
|---|---|---|
| 10 | 11 | 001 |
D: 01 недопустимо из-за того что код D совпадает с концом кода C (C: 0 0 1, D: 0 1);
| A | B | C |
|---|---|---|
| 10 | 11 | 00 |
D: 11 недопустимо из-за того что код D совпадает с кодом B (B: 11, D: 11);
| A | B | C |
|---|---|---|
| 100 | 110 | 010 |
D: 01 допустимо. Код D не совпадает ни с одним другим кодом и с окончанием никакого другого кода.
Для однозначности декодирования последовательности кодов достаточно выполнения хотя бы одного из двух вышеуказанных условий Фано:
- при выполнении прямого условия Фано цепочка кодов однозначно декодируется с начала;
- при выполнении обратного условия Фано последовательность кодов однозначно декодируется с конца.
Выбрать, какое из двух правил Фано используется при решении конкретной задача, можно, проанализировав коды в условии задачи (без учёта кода, проверяемого в вариантах ответа): если для исходных кодов выполняется прямое условие Фано, то его и нужно использовать при решении, и наоборот.
Вместе с тем нцжно помнить, что правила Фано — это достаточное, но не необходимое условие однозначного декодирования: если не выполняется ни прямое, ни обратное правило Фано, конкретная двоичная последовательность может оказаться такой, что она декодируется однозначно (так как остальные возможные варианты до конца декодирования довести не удаётся). В подобном случае необходимо пытаться строить дерево декодирования в обоих направлениях.
Рекомендуется начинать решение задач такого типа с анализа выполнимости правил Фано для исходных кодов, указанных в условии задачи (т.е. без учёта искомого кода в вариантах ответов). В зависимости от того, какое из двух правил Фано выполняется для исходных кодов, при дальнейшем решении задачи производится сравнение более короткого кода с началом (при выполнении прямого правила Фано) или с концом (при выполнении обратного правила Фано) более длинного кода.
Если для заданной последовательности кодов выполняется обратное правило Фано, то её декодирование необходимо вести с начала (слева направо). Если для заданной последовательности кодов выполняется обратное правило Фано, то её декодирование необходимо вести с конца (справа налево).
При сравнении пары кодов удобно подписывать более короткий код под более длинным, выравнивая эти записи по левому краю — для прямого правила Фано либо по правому краю — для обратного правила Фано.
Дерево Фано
Дерево Фано — это удобный и наглядный способ решения задач, связанных с подбором неравномерных двоичных кодов.
Пример кодового дерева
Исходные символы: A (частота встречаемости 50) B (частота встречаемости 39) C (частота встречаемости 18) D (частота встречаемости 49) E (частота встречаемости 35) F (частота встречаемости 24)
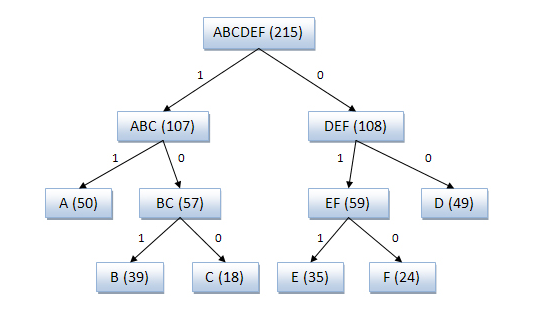
Полученный код: A — 11, B — 101, C — 100, D — 00, E — 011, F — 010.
Основные принципы построения дерева Фано
- Учёт частоты встречаемости символов в тексте — чем чаще встречается какой-либо символ, тем короче для него должен быть код и тем раньше этот символ надо поместить в дерево.
- Каждый узел дерева Фано порождает ровно две ветви (т.е. дерево Фано является бинарным), при этом одной ветви (например, левой) сопоставляется бит 0, а другой ветви — бит 1.
- На каждом новом этапе ветвления, кроме самого последнего, одна ветвь может быть завершена каким-то символом из тех, для которых генерируются коды, но вторая ветвь обязательно должна служить продолжением дерева (иначе его не удастся построить для остальных символов). Только два последних символа рассматриваемого алфавита можно поместить на концах двух последних ветвей, тем самым "закрыв" и дерево, и генерацию кодов.
- Для каждого символа код Фано получается последовательной записью всех нулей и единиц по кратчайшему пути от вершины дерева к соответствующему символу.