Теория
Системы счисления
Система счисления — знаковая система, позволяющая по определённым правилам записывать числа при помощи символов некоторого алфавита (цифр).
Позиционные системы счисления: количественные значения цифр зависят от их позиций(разрядов) в числе, что позволяет при помощи небольшого набора цифр записывать практически любые по величине числа.
Непозиционные системы счисления: значение числа получается путём суммирования(и вычитания) количественные значения цифр, не зависящих от их местоположения в числе. Например: римская система счисления.
| Римская цифра | M | D | C | L | X | V | I |
|---|---|---|---|---|---|---|---|
| Значение | 1000 | 500 | 100 | 50 | 10 | 5 | 1 |
При расшифровке римская записи числа:
- если меньшая по значение цифра располагается слева от большей, то значение меньшей цифры вычитается из значения большей;
- если меньшая по значению цифра располагается справа от большей, то значение меньшей цифры прибавляется к значению большей;
- в числе рекомендуется вначале выделить группы цифр, в которых меньшая цифра расположена левее большей, и вести расшифровку числа в несколько этапов. Пример перевод числа из римской системы счисления в десятичное число:
Основание позиционной системы счисления
Основание системы счисления определяет изменение количественного значения("во сколько раз") при изменении положения цифры в числе на один разряд правее/левее и равно количеству цифр в алфавите системы счисления.
Теоретически возможно любое значение основания системы счисления, начиная с 2. Для системы счисления с основанием p, меньше 10, в качестве знаков алфавита системы счисления используются десятичные цифры от 0 до (p - 1). Для систем с основанием p, больше 10, используются все 10 десятичных цифр плюс дополнительные символы(обычно — латинские заглавные буквы, начиная с "А"). На практике системы счисления с основанием больше 16 практически не используются (за исключением измерения времени и градусной меры углов, основанных на системе счисления с основанием 60). Обычно при записи числа значение основания системы счисления записывается в виде нижнего индекса после последней цифры числа.
Примеры наиболее часто используемых систем счисления
| Система счисления | Основание(p) | Алфавит системы счисления | Пример записи числа |
|---|---|---|---|
| Двоичная | 2 | 0,1 | 101101 |
| Восьмеричная | 8 | 0,1,2,3,4,5,6,7 | 1234567 |
| Десятичная | 10 | 0,1,2,3,4,5,6,7,8,9 | 999 |
| Шестнадцатеричная | 16 | 0,1,2,3,4,5,6,7,8,9,A=10,B=11,C=12,D=13,E=14,F=15 | F4D9 |
Формы записи чисел в различных системах счисления
Свёрнутая("обычная") форма записи числа — привычная запись числа как последовательности цифр, стоящих на своих разрядах.
Развёрнутая форма записи числа — запись числа в виде суммы произведений его цифр на основание системы счисления в степени, равной значению разряда той или иной цифры числа (для целого числа нумерация разрядов ведётся с нуля справа налево; для дробного числа нумерация разрядов ведётся от десятичной запятой влево по возрастанию, а вправо — по убыванию, при этом разряду единиц присваивается нулевой номер).
Формула (схема) Горнера — преобразованная запись развёрнутой формы, при которой за счёт использования скобок удаётся избавиться от возведения основания счисления в степени. Схема Горнера предполагает рекуррентные вычисления.
Примеры:
а) для целых чисел:
| Формы записи | Двоичное | Восьмеричное | Десятичное | Шестнадцатеричное |
|---|---|---|---|---|
| Свёрнутая | ||||
| Развёрнутая | ||||
| Схема Горнера |
б) для дробных чисел:
| Формы записи | Двоичное | Восьмеричное | Десятичное | Шестнадцатеричное |
|---|---|---|---|---|
| Свёрнутая | ||||
| Развёрнутая |
Перевод числа из недесятичной системы счисления в десятичную
Перевод числа из недесятичной системы счисления в десятичную осуществляется путём выполнения вычислений по развёрнутой записи исходного числа. Например:
- Перевести в десятичную систему счисления число 101,11:
- Перевести в десятичную систему счисления число F4D,7:
Перевод целого десятичного числа в недесятичную систему счисления
Перевод целого десятичного числа в недесятичную систему счисления выполняется путём последовательного деления числа с остатком на основание системы счисления с последующей записью полученного результата и остатков на каждом шаге деления в порядке, обратном порядку их получения. Деление производится до тех пор, пока полученный на очередном шаге результат не будет меньше основания системы счисления.
Пример: перевести число 12345 в троичную систему счисления.
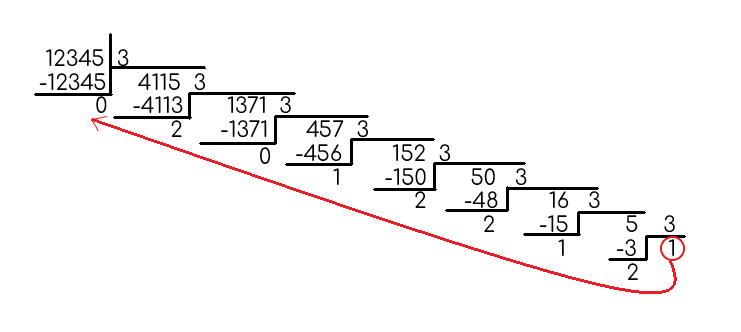
В результате:
Перевод десятичной дроби в недесятичную систему счисления
Перевод десятичной дроби в недесятичную систему счисления выполняется путём последовательного умножения числа на основание системы счисления с отбрасыванием получаемых целых частей на каждом шаге умножения и последующей записью полученных значений целых частей по порядку их получения. Умножение производится до получения значения с нулевой дробной частью либо до достижения необходимой точности представления дроби(необходимого количества значащих цифр после запятой).
Пример: требуется перевести число 0,123 в пятеричную систему счисления с точностью до 5 значащих цифр после запятой:
Представление десятичной дроби в недесятичной системе счисления, как правило, является приближённым(за исключением случаев, когда последовательность делений завершается получением нулевой дробной части либо за счёт представления дроби как периодической).
Перевод вещественного десятичного числа в недесятичную систему счисления
Перевод вещественного десятичного числа в недесятичную систему счисления выполняется в два этапа:
- Отдельно осуществляется перевод целой части числа путём последовательности делений на основание системы счисления;
- Отдельно выполняется перевод дробной части числа путём последовательности умножений на основание системы счисления.
Запись целой части числа в искомой системе счисления дополняется справа запятой и записью дробной части в искомой системе счисления. Пример: требуется перевести число 15,12 в пятеричную систему счисления с точностью до 5 значащих цифр после запятой:
В результате:
Перевод чисел между недесятичными системами счисления
Перевод чисел между недесятичными системами счисления обычно удобнее всего производить через десятичную систему счисления:
- Перевести исходное число в десятичную систему счисления;
- Перевести полученное десятичное число в требуемую систему счисления.
Перевод чисел между системами счисления с кратными основаниями
Если основания исходной и конечной системы кратны друг другу, то перевод чисел между этими системами счисления можно выполнять по упрощённой схеме.
Перевод двоичного числа в восьмеричную систему счисления
Перевод двоичного числа в восьмеричную систему счисления производится по триадам цифр:
- Исходное двоичное число разбивается на группы по три цифры(триады) справа налево; при необходимости крайняя слева группа цифр дополняется незначащими нулями слева;
- Каждая триада двоичных цифр заменяется соответствующим ей восьмеричным значением согласно таблице:
| Двоичная триада | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
|---|---|---|---|---|---|---|---|---|
| Восьмеричное значение | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Пример: требуется перевести число 1011010 в восьмеричную систему счисления: 1011010 → 001 011 010 → 1 3 2.
В результате:
Перевод восьмеричного числа в двоичную систему счисления
Перевод восьмеричного числа в двоичную систему счисления также производится по триадам цифр:
- Исходное восьмеричное число разбивается на отдельные цифры;
- Каждая восьмеричная цифра заменяется соответствующей её триадой двоичных цифр по таблице(см. выше);
- Искомое двоичное число составляется из полученных триад; Незначащие нули слева отбрасываются.
Пример: требуется перевести число 12345 из восьмеричной системы в двоичную систему счисления:
1 2 3 4 5 → 001 010 011 100 101 → 1010011100101.
В результате:
Перевод двоичного числа в шестнадцатеричную систему счисления
Перевод двоичного числа в шестнадцатеричную систему счисления производится по тетрадам цифр:
- Исходное двоичное число разбивается на группы по четыре цифры ("тетрады") справа налево; При необходимости крайняя слева группа цифр дополняется незначащими нулями слева;
- Каждая тетрада двоичных цифр заменяется соответствующим ей шестнадцатеричным значением согласно таблице:
| Двоичная триада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Шестнадцатеричное значение | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Пример: требуется перевести число 1011010 из двоичной системы счисления в шестнадцатеричную: 1011010 → 0101 1010 → 5 А. В результате:
Перевод шестнадцатеричного числа в двоичную систему счисления
Перевод шестнадцатеричного числа в двоичную систему счисления также производится по тетрадам цифр:
- Исходное шестнадцатеричное число разбивается на отдельные цифры;
- Каждая шестнадцатеричная цифра заменяется соответствующей ей тетрадой двоичных цифр по таблице (см. выше);
- Искомое двоичное число составляется из полученных тетрад; Незначащие нули слева отбрасываются.
Пример: требуется перевести число 1ADA из шестнадцатеричной системы счисления в двоичную: 1 A D A → 0001 1010 1101 1010 → 1101011011010. В результате:
При преобразовании чисел по триадам и тетрадам не забывайте дополнять триады(тетрады) незначащими нулями слева до трёх(четырёх) знаков, а также отбрасывать незначащие нули после завершения преобразования.
Таблицы степеней
Существенную помощь при вычислениях, связанных с переводом чисел в десятичную систему счисления, могут оказать таблицы значений степеней оснований системы счисления. В качестве примера приведена такая таблица для основания системы счисления, равного 2(рекомендуется выучить её наизусть). Аналогично можно составить подобные таблицы и для других оснований систем счисления.
| ... | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Значение | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | 8192 | 16384 | 32768 | ... | 1048576 |
Арифметика в недесятичных системах счисления (на примере двоичной арифметики)
Правила арифметических вычислений в общем едины для любой позиционной системы счисления. Необходима только внимательность при отслеживании переносов между разрядами, возникающих при непривычном недесятичном значении основания системы счисления.
Сложение одноразрядных двоичных чисел
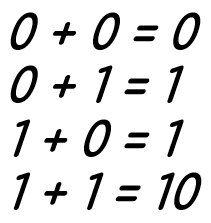
Умножение одноразрядных двоичных чисел
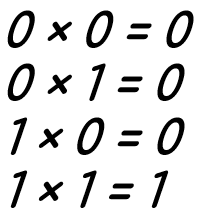
Вычитание одноразрядных двоичных чисел
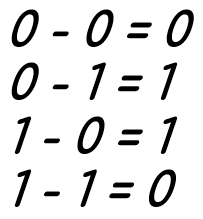
Сложение многоразрядных двоичных чисел
Выполняется в столбик. Пример: требуется сложить 1111 и 111.
Распишем поразрядно действия при сложении в столбик:
- Первый: 1 + 1 = 0 — единица переходит в следующий разряд.
- Второй: 1 + 1 + 1 = 1 — единица переходит в следующий разряд.
- Третий: 1 + 1 + 1 = 1 — единица переходит в следующий разряд.
- Четвёртый: 1 + 0 + 1 = 0 — единица переходит в следующий разряд.
- Пятый: 1 + 0 + 0 = 1.
Вычитание многоразрядных двоичных чисел
Выполняется в столбик, при этом возможен заём единицы из старшего разряда. Пример: требуется вычислить значение выражения 110101 - 1001:
Умножение многоразрядных двоичных чисел
Выполняется в столбик аналогично умножению десятичных чисел. Однако при этом для двоичной системы счисления можно воспользоваться следующими простыми правилами:
- Всегда умножать большее число на меньшее;
- Умножение заменяется сложением копий множимого числа, записанных друг под другом со сдвигом каждый раз на одну позицию влево для каждого единичного разряда множителя (для нулевых разрядов множителя копии множимого в искомой сумме пропускаются).
Пример: требуется вычислить значение выражения 110101 × 1101(для 2-го нулевого разряда копия множимого пропускается):
Деление многоразрядных двоичных чисел
Выполняется аналогично делению в столбик десятичных чисел. При этом на каждом шаге деления выполняется последовательное вычитание делителя из очередного делимого до получения остатка, равного 0 или 1, а подсчитанное количество вычитаний записывается как очередное значение частного.
Пример: требуется вычислить значение выражения 10010 / 110.
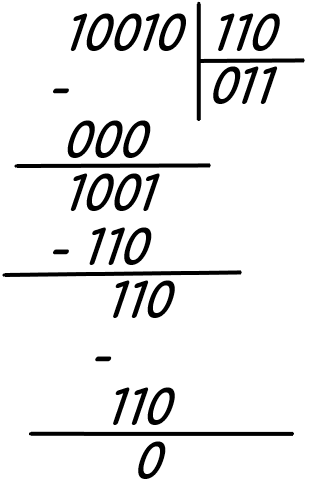
Пошаговый алгоритм:
- Первые три числа делимого меньше, чем делитель — значит, умножаем делитель на 0 и вычитаем. Получаем 100.
- Дописываем 1 справа от 100, видим, что 1001 больше, чем 110, поэтому умножаем делитель на 1 и вычитаем его из 1001. Получаем 11.
- Дописываем 0 справа. Полученное 110 равно делителю, поэтому тоже умножаем его на 1, получаем конечный результат.
В результате: 10010 / 110 = 11.
Ещё пример: требуется вычислить значение выражения 1100 / 10.
Пошаговый алгоритм:
- Смотрим на делимое, видим, что первые две его цифры — 11. Умножаем делитель на 1 и вычитаем из 11 число 10.
- Получили 1, дописываем справа следующую по порядку цифру — 0. Теперь 10 равно делителю, значит, тоже умножаем его на 1 и вычитаем.
- Получаем 0. Но у нас ещё остался один 0 у делимого — дописываем его справа от полученного 0.
- Число 0 меньше, чем 10, поэтому умножаем делитель на 0.
В результате: 1100 / 10 = 110.
Арифметические операции в других системах счисления выполняются аналогично.
Для упрощения расчётов и исключения возможных ошибок при выполнении арифметических операций в недесятичных системах счисления рекомендуется вначале перевести все числа-операнды в десятичную систему счисления, выполнить расчёты в ней, а затем выполнить перевод результата в искомую систему счисления. Незначащими в записи числа являются только нули, стоящие слева от числа(которые не влияют на числовое значение и могут быть отброшены). Все остальные нули и единицы в записи числа являются значащими!