Внимание!На странице используются подгружаемые формулы. Пожалуйста, перезагрузите страницу если зашли первый раз!
Теория измерения информации
Вероятностный подход к измерению количества информации
Для определения количества информации, содержащейся в сообщении о каком-либо объекте или событии, используется вероятностный подход. Он основан на следующих соображениях:
- те или иные события имеют некоторую вероятность произойти или не произойти;
- событие, которое совершается всегда, имеет вероятность равную 1(или 100%);
- событие, которое не совершается никогда, имеет вероятность, равную 0 (или 0%);
- в остальных случаях вероятность совершения события есть дробное число от 0 до 1;
- получая сообщение о совершении (или несовершении) некоторого события, создаётся некоторое количество информации, которое определяется снятой с её помощью неопределённости знаний об указанном событии:
- если вероятность совершения события точно равна 1 или 0(т.е. мы точно знаем, что событие произойдёт или не произойдёт), то никакой неопределённости в наших знаниях нет и сообщение о таком событии несёт практически нулевое количество информации;
- для равно вероятностных событий чем больше их количество(т.е. шире возможный выбор вариантов и потому меньше вероятность каждого из них), тем большее количество информации несёт сообщение о совершившемся конкретном событии;
- количество информации в сообщении о совершении(несовершении) нескольких независимых событий равно сумме количеств информации, содержащейся в сообщениях о каждом отдельном таком событии.
Формула Хартли
Для N равновероятностных возможных событий количество информации, которое несёт сообщение о выборе (совершении) одного конкретного события, определяется формулой Хартли:
| N | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | 8192 | 16384 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i(бит) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
Для значений N, не равных степени двойки, при определении количества информации в битах из выше приведённой таблица берётся ближайшее большее значение N, равное степени 2.
"Принцип вилки"
Для приближённого вычисления количества информации при значении N, не равном 2 в некоторой степени, определяются значения количества информации для двух соседних значений N, составляющих степени 2, и составляется соответствующее двойное неравенство.
Например, пусть нужно оценить количество информации в сообщении о выпадении на верхней грани игрального кубика шести точке. В этом случае N = 6. Ближайшим к нему являются значения — степень двойки: N = 4 (2 * 2) и N = 8 (2 * 2 * 2). Тогда можно составить неравенство:
Формула Шеннона
Связь количества информации с понятием вероятностей первым определил в своей формуле Клод Шеннон. Для событий с различными вероятностями p1, p2, ..., pn количество информации определяется формулой Шеннона:
Если все события равновероятны, т.е. p1 = p2 = ... = pn = p, то очевидно, что формула Шеннона преобразуется в формулу Хартли (которая, таким образом, представляет собой частный случай формулы Шеннона).
Связь между количеством информации и вероятностью события
Для N равновероятных событий вероятность одного отдельного события p = 1/N. С учётом этого формула Хартли может быть преобразована в соотношение:
"Принцип ёлочки"
Сколько информации несёт в себе некоторое сообщение? Известно, что количество информации, равное 1 биту, соответствует снятию неопределённости при помощи ответа "да" или "нет", на один элементарный вопрос, т.е. 1 бит соответствует уменьшению неопределённости в 2 раза. А чему соответствует уменьшение неопределённости, например, в 4 раза? В подобном случае можно задать последовательно два вопроса, на количество информации в n бит позволяет уменьшить неопределённость в 2 в степени n раз.
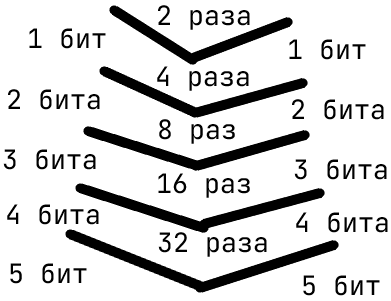
Величины информации
Принято считать, что минимально возможное количество информации соответствует такому сообщению, получение которого уменьшает неопределённость в 2 раза (пример — сообщение о выпадении на подброшенной монете "орла" и "решка"). Это минимальное количество информации получило название "бит"(англ. bit как сокращение названия binary digit — двоичная цифра).
В вычислительной технике бит соответствует одному двоичному разряду, который может принимать одно из двух значений: 0 или 1. В качестве более крупной величины принят "байт", соответствующий двоичному числу из 8 разрядов(битов). В оперативной памяти компьютера минимальный объём ячейки памяти, выделяемой для хранения какой-либо величины, как правило, минимум равен одному байту. Ячейки большего размера имеют объём, кратный байту с коэффициентом кратности 2: 2 байта (16 битов), 4 байта (32 бита), 8 байтов(64 бита). Такую "порцию" информации принято называть машинным словом.
В теории информации количество информации может быть дробной величиной. В вычислительной технике количество информации может составлять только целое число битов. Обычно в большинстве задач получаемое количество битов округляется в большую сторону до целого количества байт.
Для обозначения количества информации, больше чем байт, приняты следующее обозначения:
| Название | Обозначение | Степень |
|---|---|---|
| байт | Б|B | |
| килобайт | Кбайт|KB | |
| мегабайт | Мбайт|MB | |
| гигабайт | Гбайт|GB | |
| терабайт | Тбайт|TB | |
| петабайт | Пбайт|PB | |
| эксабайт | Эбайт|EB | |
| зеттабайт | Збайт|ZB | |
| йоттабайт | Ибайт|YB |
В отличие от одноимённых приставок в кратных величинах в математике/физике(СИ) изменение величин в вычислительной технике(МЭК) происходит на каждом "шаге" вышеуказанной таблицы на 1024, а не на 1000.
Алфавитный подход к измерению количества информации
Алфавит. Мощность алфавита
В этом случае количество информации в сообщении представляет собой чисто технический параметр (важный с точки зрения хранения или передачи информации) и не зависит от содержания сообщения.
При алфавитном подходе информационное сообщение рассматривается как некоторое количество (К) знаков (символов, кодов) из некоторого используемого полного набора, называемого алфавитом. Количество (N) знаков в алфавите называется мощностью этого алфавита.
В конкретном сообщении не обязательно используются все знаки алфавита. Мощность алфавита определяется не набором знаков, используемых в конкретном сообщении, а количеством знаков, которые вообще могут быть использованы в сообщениях, кодируемых в соответствии с данным алфавитом.
Алгоритм определения количества информации в сообщении:
- Определяется мощность используемого алфавита N;
- Определяется количество информации, приходящееся в алфавите на один его знак:
- если использование всех знаков равновероятно, то используется формула Хартли
- если известны вероятности использования тех или иных знаков (на основе составленной таблицы частоты встречаемости этих знаков), то используется формула Шеннона.
- Вычисленное количество информации, приходящееся на один знак(I), умножается на количество знаков в сообщении(K):
Обобщённая схема решения задач на определение количества информации с использованием алфавитного подхода
В пароле используются буквы, цифры и/или символы
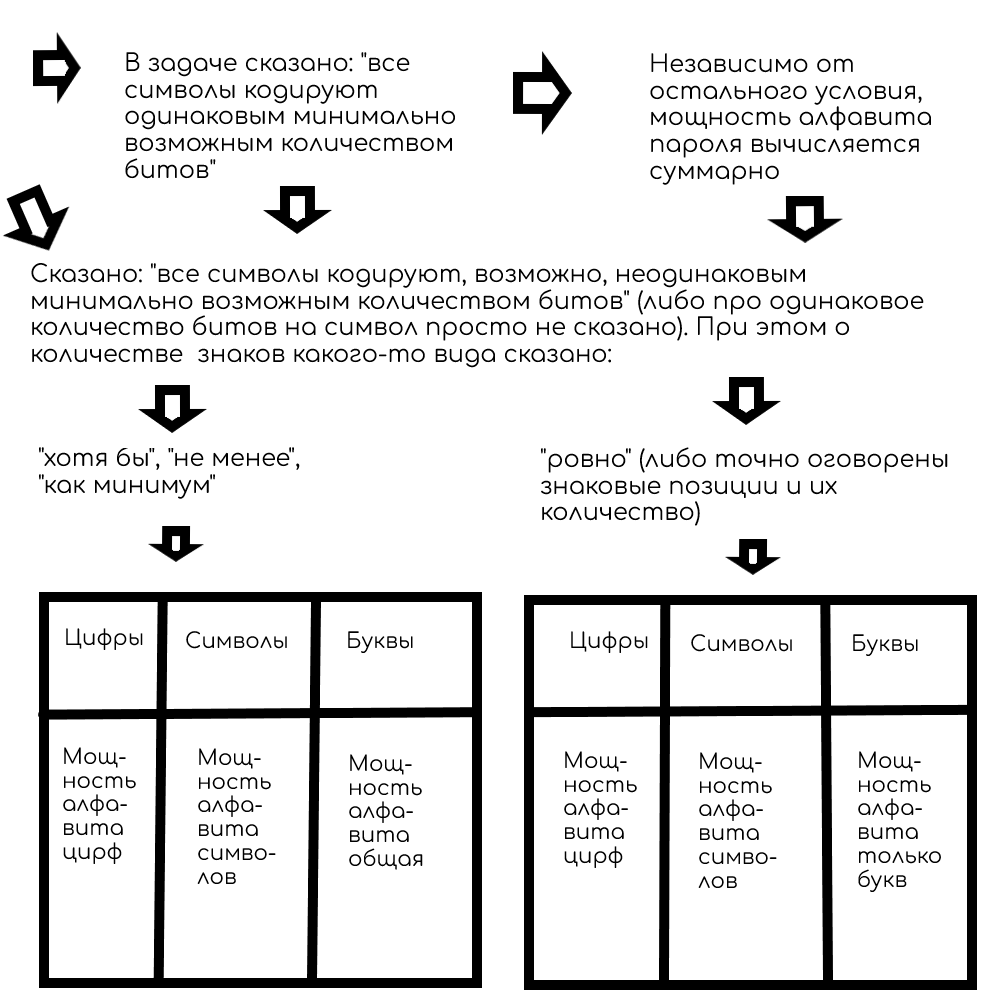
В пароле используются числа
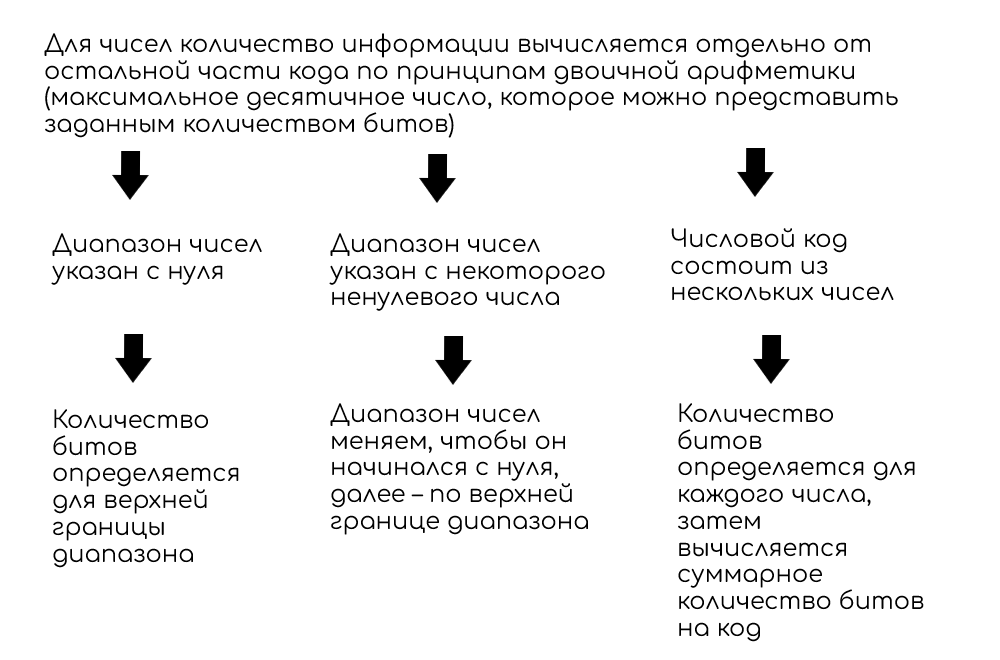
Количество различных состояний панели, имеющей М элементов, каждый из которых может находиться в N различных состояниях, равно количеству различных М-разрядных чисел (начиная с нуля) в системе счисления с основанием N и вычисляется как:
Количество различных сообщений, включающих в себя M элементов, каждый из которых может иметь N различных состояний, равно количеству различных M-разрядных чисел (начиная с нуля) в системе счисления с основанием N и вычисляется как:
Количество всех M-разрядных чисел в системе счисления с основанием N равно:
Максимальное значение M-разрядного числа в системе счисления с основанием N равно:
Если в условии задачи предлагается определить количество сигналов, подаваемых с помощью разного количества элементов (от X до Y), то нужно отдельно вычислить количества возможных сигналов для каждого возможного числа элементов и просуммировать полученные значения.